§2.5
高阶导数
我们知道,变速直线运动的速度![]() 是位置函数
是位置函数![]() 对时间
对时间![]() 的导数,即
的导数,即![]() 或
或 ![]() 。
。
而加速度
![]() 又是速度
又是速度 ![]() 对时间
对时间 ![]() 的导数,即
的导数,即
![]() 或
或 ![]()
这种导( 函 )数的导数![]() 或
或 ![]() 叫做
叫做![]() 对
对![]() 的二阶导数,记作
的二阶导数,记作
![]() 或
或 ![]() 。
。
一、高阶导数的定义

相应地,把![]() 的导数
的导数![]() 叫做函数
叫做函数![]() 的一阶导数。
的一阶导数。
类似地,
二阶导数的导数,叫做三阶导数,三阶导数的导数叫做四阶导数,…,一般地,![]() 阶导数的导数叫做
阶导数的导数叫做 ![]() 阶导数,分别记作
阶导数,分别记作
![]()
或 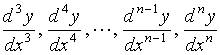 。
。
函数![]() 具有
具有![]() 阶导数,称函数
阶导数,称函数![]() 为
为![]() 阶可导的;如果函数
阶可导的;如果函数![]() 在点
在点![]() 处具有
处具有![]() 阶导数,那未
阶导数,那未![]() 在点
在点![]() 处的某一邻域内必具有一切低于
处的某一邻域内必具有一切低于![]() 阶的导数。
阶的导数。
二、几个基本的高阶导数公式
【公式1】![]()
证明:记 ![]()
![]() ,
, ![]() , … ,
, … ,
一般地 ![]()
【特款】当
![]() 时,
时,![]()
【公式2】 ![]()
证明:
记 ![]()
![]()
![]()
![]()
一般地有![]()
【特款】![]()
证明:![]()
![]()
利用上面得到的![]() 阶导数公式有
阶导数公式有
![]()
【公式3】![]()
证明: ![]()
![]()
![]() , 一般地有:
, 一般地有:
![]()
【特款】当
![]() (
( ![]() 为正整数 ) 时, 有
为正整数 ) 时, 有
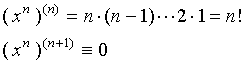
【公式4】 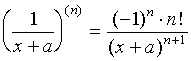 (
(![]() 为实数 )
为实数 )
证明: 记 ![]()
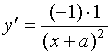

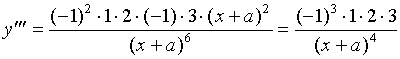
一般地,
有
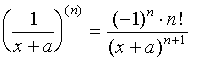

这一公式的证明与中学的二项展开公式的证明完全类似,同学们可与之对应起来看。
证明:当![]() 时,(1)式显然成立。
时,(1)式显然成立。
假设当![]() 时,(1)式仍然成立,即:
时,(1)式仍然成立,即:
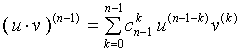
于是有
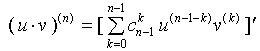
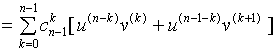
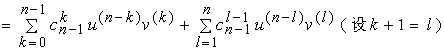
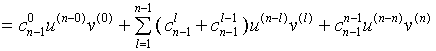
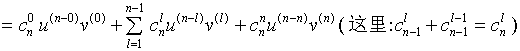
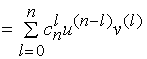
三、求函数高阶导数举例

【例1】求函数 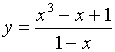 的
的 ![]() 阶导数。
阶导数。
解:
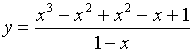
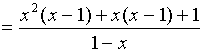
![]()
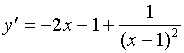
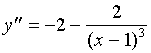
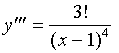
当
![]() 时, 有
时, 有
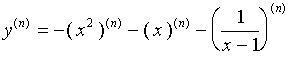
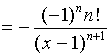

【例2】设![]() , 求
, 求 ![]() 。
。
解:利用莱布尼兹公式,有
![]()
![]()
![]()
![]()